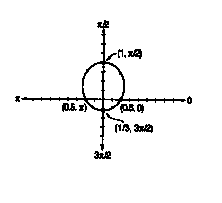Article Review
for
Germain-McCarthy, Yvelyne. "Circular Graphs: Vehicles for Conic and Polar Connections." The Mathematics Teacher, January 1995. Vol.88 No.1: 27.

This article discusses an alternative method for teaching conic sections in polar coordinates. The goal of this method is to unify more clearly in the students' minds the relationship between conic sections and polar equations. While many Calculus books teach that the reciprocals of limaçons are in fact conic sections, most prove this fact algebraically disregarding the "inherent connection between polar graphs and the graphs of trigonometric functions" with regard to conics. This alternative method gives students a better appreciation of the many ways in which a problem can be solved.
The method consists of a student working several examples involving each conic section in order to recognize a conic section by it's auxiliary graph. This will establish the relationship between the auxiliary and the conic section. In order to accomplish this a student must understand the relationship between the graphs y = A - Bsin x and r = A - Bsin . It should be understood that the y and r values are the same and that the x and values are the same. Thus the equation y = A - Bsin x can serve as a table for the equation r = A - B sin . This is key concept that must be understood for the method to make sense for the student.
For each example the student undertakes there are two graphs to be constructed. First, the student must make an auxiliary graph of y=1/(A - B sinx). Then, they must construct the polar graph r=1/(A - B sin ) by using the auxiliary as a table of values. Before actually constructing the polar graph, the student should make predictions of what the polar graph will look like. For example, the equation y=1/(2 - sinx) is graphed both in its auxiliary form and polar form ( r=1/(2 - sin )). The graphs taken from the article are seen below.



The student must make observations from the auxiliary graph. There are several key points on the graph which are shown above. It should be noticed that r will start at 0.5, increase to 1 at /2 and then decrease to 1/3 at 3 /2. It will finally conclude with r= 1 at 2 . When this knowledge is applied to the polar graph (see above) it is shown that this polar equation creates an ellipse.
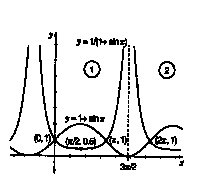
The next example uses the equation y=1/(1+sinx) and r=1/(1+sin ). The graphs taken from the article are seen below.



The student once again must graph the auxiliary and notice the key points before graphing the polar graph. The auxiliary graph is divided into two sections. From the first section it can be determined that r=1 at 0 decreases to 0.5 at /2 then increases infinitely as it approaches 3 /2. This fact explains why the polar graph remains open at 3 /2 radians. Then a look at section 2 of the auxiliary graph shows that r starts infinitely large at 3 /2 then decreases to 1 at 2 thus making the polar graph a parabola.
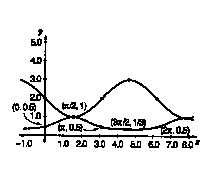
The final example used in the article involves the auxiliary graph y=1/(1+2sinx) and the polar graph r=1/(1+2sin ). The graphs from the article are seen below:



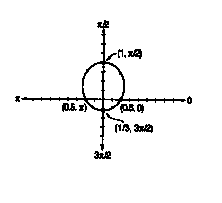
This time the auxiliary graph is divided into three sections with section two of the graph giving negative y values. A look at certain key points shows that the polar graph begins with r=1, decreases to 1/3 at /2 and increases infinitely at 7 /6. Then in section 2 the r values are reflected radians so that they are graphed in the range of /6 to 5 /6 instead of 7 /6 to 11 /6. In this section, r is very large at 7 /6 (or /6 on the polar graph), decreases to 1 at 3 /2 ( /2) and then becomes very large again as it approaches 11 /6 (5 /6 polar). Finally, in the third section the r is very large at 11 /6 and decreases to 1 at 2 . Upon completion of the graph the student should realize that r=1/(1+2sin ) is a hyperbola.
The author of this article believes that after a few more examples students will understand the relationship between the auxiliary graph and its polar complement. Thus, this exercise not only teaches more about conics, it teaches students there are alternative ways to solve problems.